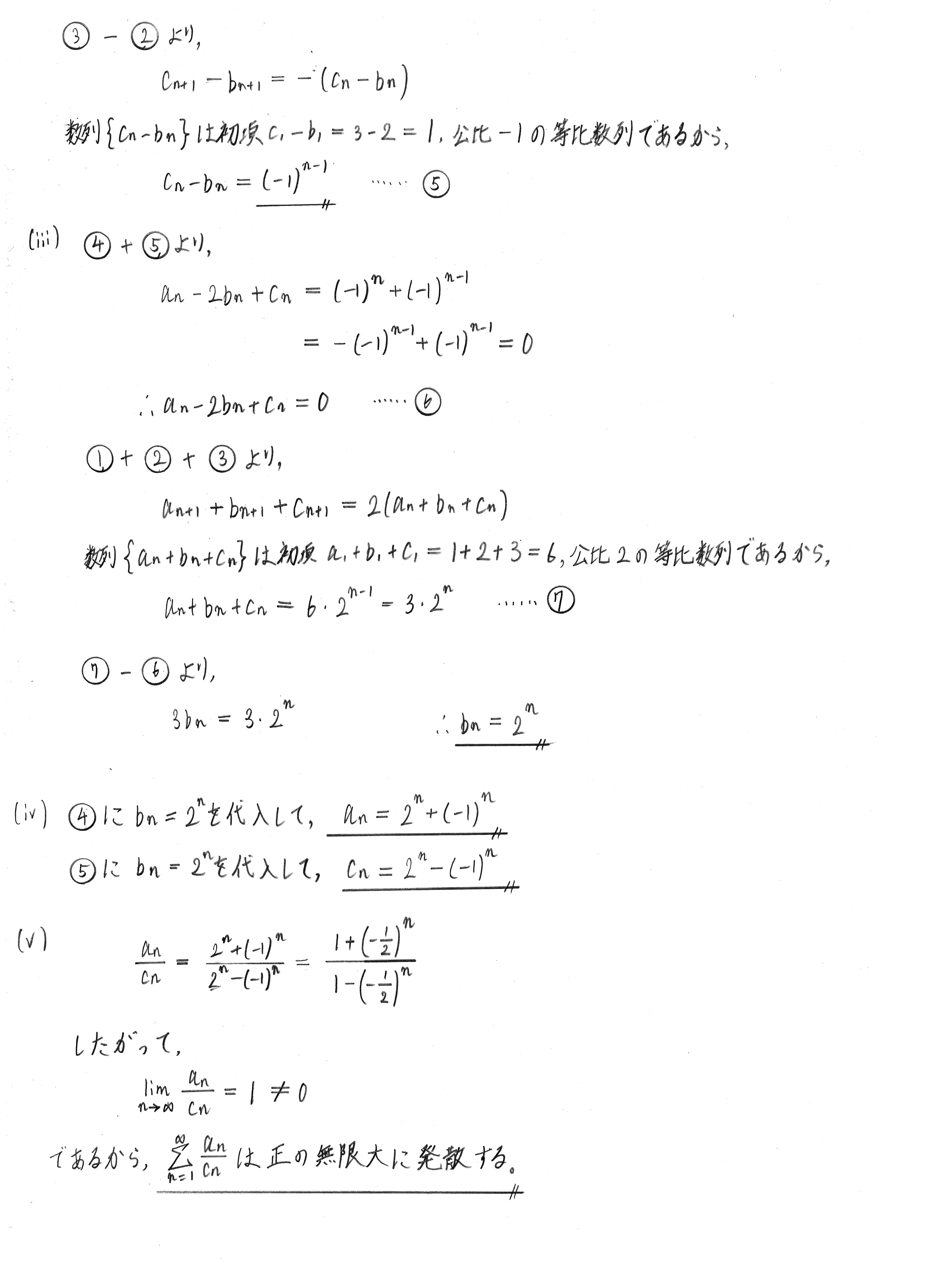問題4

次の条件によって定められる数列$\; \{a_n\}, \{b_n\}, \{c_n\}\;$を考える。

$$a_1 = 1,\qquad a_{n + 1} = b_n + c_n \qquad (n = 1, 2, 3, \cdots \cdots)$$ $$b_1 = 2,\qquad b_{n + 1} = c_n + a_n \qquad (n = 1, 2, 3, \cdots \cdots)$$ $$c_1 = 3,\qquad c_{n + 1} = a_n + b_n \qquad (n = 1, 2, 3, \cdots \cdots)$$

このとき，以下の問いに答えよ。

(配点 50)

(i) $\; a_2, b_2, c_2\;$を求めよ。

(ii) $\; a_n - b_n,\; c_n - b_n\;$をそれぞれ$\; n\;$の式で表せ。

(iii) 数列$\; \{b_n\}\;$の一般項を求めよ。

(iv) 数列$\; \{a_n\}\;$の一般項と数列$\; \{c_n\}\;$の一般項を求めよ。

(v) 無限級数$\; \dis{\sum_{n = 1}^\infty \frac{a_n}{c_n}}\;$の収束，発散について調べ，収束するときにはその和を求めよ。